Previously, shadow maps were added to the game. However, the game still had a feeling of being a bit too flat. This is because shadow mapping only accounts for the occlusion of one object by another. It does not simulate the effect of objects being darker at grazing angles to a source of light. If you have a window near you, open the palm of your hand towards it. It should be maximally bright. Once you start rotating your palm away from the light – even without occluding your hand by itself – you’ll notice your hand darkens.

Diffuse lighting

This is actually much easier to model than shadow maps. For diffuse lighting, all we need is a normal (n^\hat{n}) and the direction of the light source (l^\hat{l}). With these, we want some function f(n^,l^)f(\hat{n}, \hat{l}) where:

f(n^,l^)=0f(n^,l^)=1\begin{align*} f(\hat{n}, \hat{l}) = 0 \tag{when $\hat{n} \perp -\hat{l}$} \\ f(\hat{n}, \hat{l}) = 1 \tag{when $\hat{n} = -\hat{l}$} \\ \end{align*}

This is essentially the dot product, except the sign of the light direction needs to be flipped. It’s easier to work with the direction to the light rather than from the light. For angles greater than 90°90\degree, the value is less than zero, so we simply use the built in WGSL clamp function to ensure our ratio is between zero and one1.

Transforming the normal

Next, we will need the normal in world space to compare it to the light direction, which is defined in world space. Moving a vertex into world position requires multiplying it by the model matrix. However, the normal should not be affected by translation, so we should zero out the first 3 elements of the last column in the model matrix. This resultant matrix would be sufficient for use in this game, but consider the case below:

A valid model transform may scale some object along one axis, such as the yy-axis in the example above. However, this results in the transformed normal, nt^\hat{n_t}, being incorrect. We need some new normal, nw^\hat{n_w}. So, we need some other matrix to correct the potential change of the original normal. First, we need to introduce some symbols:

Symbol Description
MM Model matrix
NN Unknown matrix to correctly transform our normal, n^\hat{n}
t^\hat{t} Tangent to the normal in local space (represents a vector along any arbitrary plane of the model)
tw^\hat{t_w} Tangent after the transformation by the model matrix (in other words, in world space)

So, from the definitions we have:

nw=Nntw=Mt\begin{align*} n_w = Nn \\ t_w = Mt \end{align*}

We want to determine the transformation matrix, NN, that ensures the transformed normal and transformed tangent (nwn_w and twt_w) are perpendicular:

0=nw^.tw^0=(nw)Ttw0=(Nn)T(Mt)0=(nTNT)(Mt)0=nT(NTM)t\begin{align*} 0 &= \hat{n_w}.\hat{t_w} \\ 0 &= (n_w)^Tt_w \tag{as matrices} \\ 0 &= (Nn)^T(Mt) \\ 0 &= (n^T N^T)(Mt) \\ 0 &= n^T(N^TM)t \\ \end{align*}

By definition, nTt=0n^Tt = 0. So, we know that NTMN^TM must be the identity matrix (II). This means we can determine the transform we need, NN, as:

NTM=INT=M−1N=(M−1)T\begin{align*} N^TM &= I \\ N^T &= M^{-1} \\ N &= (M^{-1})^T \\ \end{align*}

I read this as the “inverse transpose model matrix”. The LearnOpenGL article excludes this derivation, but derivation/proof tends to help me retain information for longer. There are a few resources that explain this in a few different ways, so I’ll list them here:

  1. https://www.lighthouse3d.com/tutorials/glsl-12-tutorial/the-normal-matrix/
  2. https://en.wikipedia.org/wiki/Normal_(geometry)#Transforming_normals

The one thing these resources both mention is that the inverse transpose is equal to the original matrix if the original is an orthonormal matrix (because M−1=MTM^{-1} = M^T).

This follows from the intuition at the beginning. If only uniform scaling and rotation is applied, then it is the model matrix (without the translation). Note, however, that scaling removes the orthonormality of the matrix – so, we have to normalize the resultant vector to ensure the normal is a normal.

Putting it all together

With all of this, we have enough theory established to implement the diffuse lighting in the game. In summary, we need to make the following changes:

  1. Add the light direction to the uniforms.
  2. Add the model inverse transpose matrix (NN) to the instance buffer.
  3. Add the normal to the Vertex class and the vertex buffer (Make changes as necessary to the constructor and methods that create vertices).
  4. Use all of the above to calculate the diffuse factor and apply it to the shadow factor2.

If you’ve been following along, consider trying the above for yourself. Previous posts have covered similar changes. Otherwise, for the full change, see the link to the Git tree below. For a comparison, here is the before-and-after for the game with and without shadows and diffuse lighting:

Before After
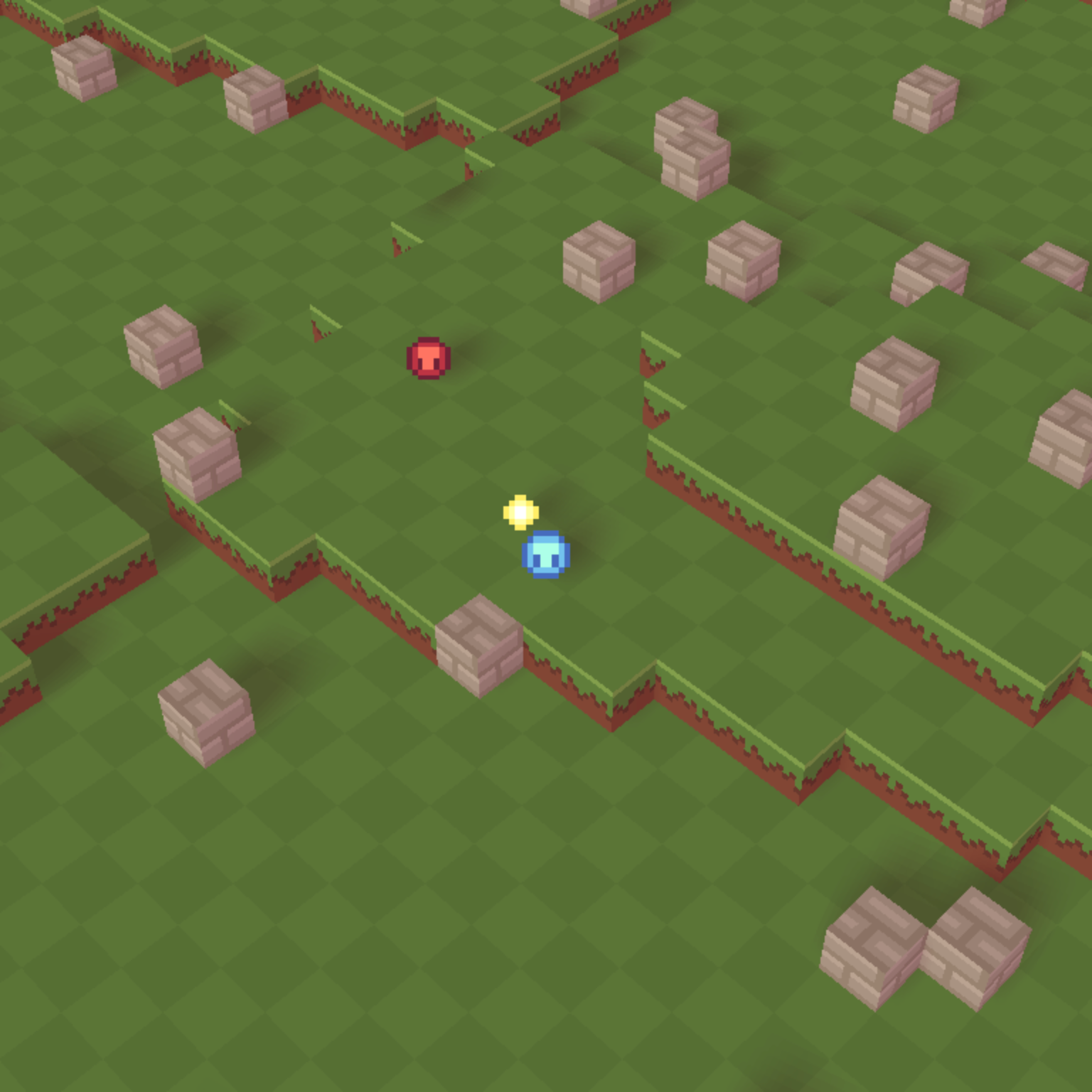Before the changes With diffuse lighting and shadows
  1. Git tree

Footnotes

  1. There are many resources for this on the internet, for example: https://learnopengl.com/Lighting/Basic-Lighting. ↩

  2. I used multiplication. It may actually make more sense to use the minimum of the two factors. ↩